Economics has never been my kind of subject, to say the least. All talk. No application to real life. That’s the way I saw it. However all that changed when I come across this fascinating world of Behavioral Economics. It seems the sole reason this subject exists is to refute, reject, destroy everything we have known to be true from classical economics and I love it for that! The beauty of this all is that the ones challenging these principles are Nobel Prize winners of our time and that too in Economics. So if you didn’t pay heed to Economics in class don’t worry because you probably didn’t need to. It’s all outdated anyways! Well not completely but you will see what I mean in a bit.
Economics is a subject rich in theories. From Keyne’s Law to Marx’s Theories. It’s full of concepts that explain how our society and economy work. One such concept is the expected utility theory. It’s an evolution of thinking about wealth beyond the value of money to the utility a certain value of money brings. This concept was introduced by Daniel Bernoulli in 1738. The idea behind this theory is simple. Let’s say the utility of 1 million is 10. Any increase in wealth is likely to increase the utility, perhaps exponentially, but to a certain point. For example, increasing wealth to 2 million increases the utility by 20 to reach 30. On the other hand, if you have wealth worth 9 million it’s utility is 96. Adding another 1 million at this level of wealth does not increase utility by much. It only increases by 4. So now with 10 million worth of wealth utility is 100. In summary this theory factors in the diminishing utility of wealth which seems very sound and logical. See the table below that illustrates this same ratio of wealth to utility.
Now let’s look at a scenario where we have two individuals – Anthony and Betty. Anthony has 1 million and Betty has 4 million and they are both given two options.
- Gamble – Equal chance to end up owning either 1 million or 4 million
- Sure-Shot – Settle for 2 million
How do you think they will make their choice? The gamble is clearly worth more than the sure shot, valued at 2.5 million (50% of 1 million + 50% of 4 million). From an economic perspective both should go for the gamble. But do they? From Anthony’s perspective if he gambles he may either end up retaining one million or quadrupling his wealth. Alternately if he went for the sure thing he would still at least double his wealth! Not wanting to take the chance Anthony may settle for the sure thing despite the probability of the gamble being higher. He would do so because if he lost the gamble the regret of not taking the sure shot and losing that extra one million would be too disappointing. On the other hand for Betty if she gambled she has a 50% chance of losing three fourth of her wealth or (if she got lucky) lose nothing! While the sure shot option is simply not for her as she would be simply giving up half her wealth. In her case she is more likely to take her chances because there is a possibility that she loses nothing. From an expected utility theory perspective both individuals should make the same choice. However where this theory fails is it’s ability to incorporate the reference point of each person. This is the theory that was developed jointly by Amos Tversky and Daniel Kahneman. It is known as the prospect theory and it basically builds on the expected utility theory by incorporating the importance of a reference point in decision making. Every decision is made from one’s reference point and the choice one is making looks at whether one is gaining or losing from where they stand. The second major breakthrough was the understanding of how we are more averse to losses than we are to gains which also explains the difference in the decisions made by Anthony and Betty.
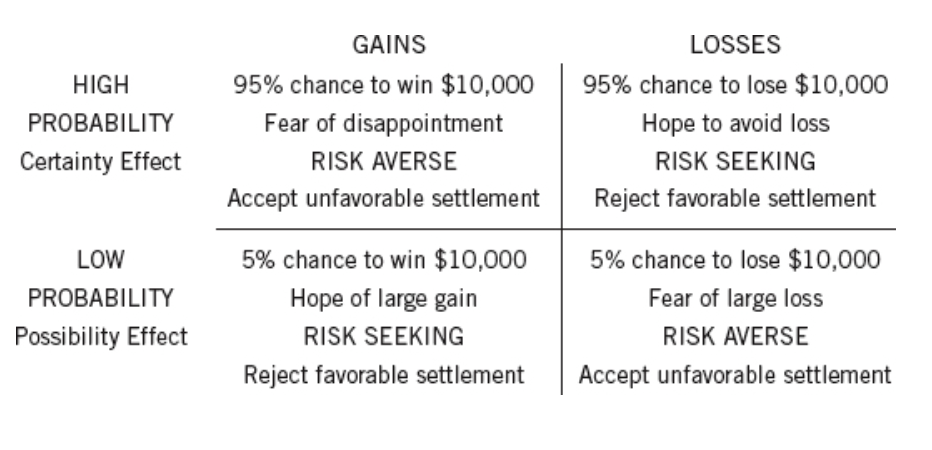
This idea of “loss aversion” affects our decision in one other aspect. How we react to risk. In absolute terms a 5% change in probability is exactly what it is – a 5% change in probability. At least as far as classic expectation principle goes. However from the context of a loss aversive mindset this change can mean something completely different. Let’s say our chances of winning $1 million improve from 0% to 5% in one case and from 95% to 100% in another case. According to the expectation principle our utility of winning $1 million increased by 5% in both cases. However a change from 0% to 5% is not the same as a change from 95% to 100%. The first case is a possibility effect. Now there is a chance to win. The change from 95% to 100% is a certainty effect. The win is certain. Depending on the situation, when one is evaluating options these two effects come into play and we end up either overweighting or underweighting our choice.
Possibility of Winning and Losing
Imagine a situation where the situation is framed as such. You are offered two options in a court of law. You have the going against you. There is a 5% chance that things will go in your favor and if they do you would gain $100,000. However you have another option to settle out of court and go for $50,000 straight away. The probability clearly favors that you settle (5% of $100,000 = $5000 vs. $50,000 for the sure shot gain) but owing to the possibility effect you will overweight that choice and not go for the safe option. Here is a case when you are being risk seeker. The pain of a loss (in this case the possibility of foregoing the extra $50,000) by accepting a seemingly compromise deal makes you go for the obviously risky choice.
Alternatively you are in another situation where you have a 5% chance to lose $100,000 or take a sure shot loss of $50,000. Probability clearly dictates that the gamble is worth $5000 but the fear of a large loss makes you risk averse and here instead of clearly going for the gamble you accept an unfavorable settlement. How the possibility of winning made you take a risk when the sure shot outcome was better and the possibility of loss made you take the unfavorable settlement while the real probability of that incident occurring was very low.
Certainty of Winning and Losing
Now let’s look at another situation. Here you are in a situation where there is a 95% chance that you would gain $100,000. If you look at the probability of winning it is $95,000 vs a settlement of $50,000. The certainty of $50,000 is overweighted and the fear of disappointment makes you risk averse. At the same time if you have 95% chance of losing $100,000 you should surely settle and stop your loss at $50,000. But the certainty of loss is underweighted this time again and in the hope of avoiding a loss you take the gamble and become a risk seeker. These scenarios have been captured in the table below.
The key lesson from it all is our deep aversion to losses and how they can cloud our judgement to clearly make the unfavorable choice. From an economic perspective, logic states otherwise but the fear of regret and disappointment loom larger in our decision making and blind us from making the right choice. This has huge implications to our life especially when it comes to litigation. You can imagine how unfavorable settlements are accepted when someone clearly has a winning case at hand and how losses that could have been avoided if the risks were taken but are not because of the fear of losing.
Feature image by SuperFantastic used under Creative Commons License 2.0